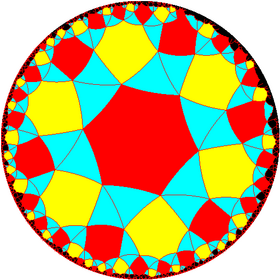
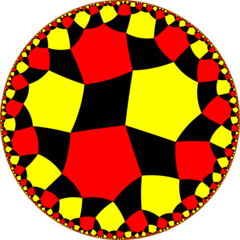
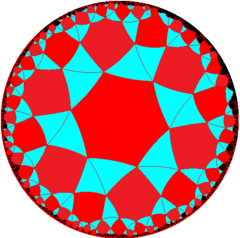
Snub hexahexagonal tiling
In geometry , the snub hexahexagonal tiling is a uniform tiling of the hyperbolic plane . It has Schläfli symbol of sr{6,6}.
Images
Drawn in chiral pairs, with edges missing between black triangles:
Symmetry
A higher symmetry coloring can be constructed from [6,4] symmetry as s{6,4},
Uniform hexahexagonal tilings
Symmetry: [6,6], (*662)
{6,6} t{6,6} 2 {4,6}
r{6,6} t{6,6} 2 {4,6}
{6,6} rr{6,6} tr{6,6}
Uniform duals
V66
V6.12.12
V6.6.6.6
V6.12.12
V66
V4.6.4.6
V4.12.12
Alternations
[1+ ,6,6]
[6+ ,6]
[6,1+ ,6]
[6,6+ ]
[6,6,1+ ]
[(6,6,2+ )]
[6,6]+
h{6,6}
s{6,6}
hr{6,6}
s{6,6}
h{6,6}
hrr{6,6}
sr{6,6}
Uniform tetrahexagonal tilings
Symmetry : [6,4], (*642 )
{6,4}
t{6,4}
r{6,4}
t{4,6}
{4,6}
rr{6,4}
tr{6,4}
Uniform duals
V64
V4.12.12
V(4.6)2
V6.8.8
V46
V4.4.4.6
V4.8.12
Alternations
[1+ ,6,4]
[6+ ,4]
[6,1+ ,4]
[6,4+ ]
[6,4,1+ ]
[(6,4,2+ )]
[6,4]+
h{6,4}
s{6,4}
hr{6,4}
s{4,6}
h{4,6}
hrr{6,4}
sr{6,4}
References
See also
External links