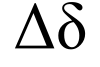en Delta (letter)

Delta (/ˈdɛltə/;^[1] uppercase Δ, lowercase δ; Greek: δέλτα, délta, [ˈðelta])^[2] is the fourth letter of the Greek alphabet. In the system of Greek numerals it has a value of 4. It was derived from the Phoenician letter dalet 𐤃.^[3] Letters that come from delta include Latin D and Cyrillic Д.

A river delta (originally, the delta of the Nile River) is so named because its shape approximates the triangular uppercase letter delta. Contrary to a popular legend, this use of the word delta was not coined by Herodotus.^[4]

Pronunciation

In Ancient Greek, delta represented a voiced dental plosive IPA: [d]. In Modern Greek, it represents a voiced dental fricative IPA: [ð], like the "th" in "that" or "this" (while IPA: [d] in foreign words is instead commonly transcribed as ντ). Delta is romanized as d or dh.

Uppercase

The uppercase letter Δ is used to denote:

Change of any changeable quantity, in mathematics and the sciences (in particular, the difference operator^[5]^[6]); for example, in ${\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}={\frac {\Delta y}{\Delta x}},$ the average change of y per unit x (i.e. the change of y over the change of x). Delta is the initial letter of the Greek word διαφορά diaphorá, "difference". (The small Latin letter d is used in much the same way for the notation of derivatives and differentials, which also describe change by infinitesimal amounts.)
The Laplace operator:
$\Delta f=\sum _{i=1}^{n}{\frac {\partial ^{2}f}{\partial x_{i}^{2}}}.$
The discriminant of a polynomial equation, especially the quadratic equation:^[7]^[8]
$\Delta =b^{2}-4ac.$
The area of a triangle
$\Delta ={\tfrac {1}{2}}ab\sin {C}.$
The symmetric difference of two sets.
A macroscopic change in the value of a variable in mathematics or science.
Uncertainty in a physical variable as seen in the uncertainty principle.
An interval of possible values for a given quantity.
Any of the delta particles in particle physics.
The determinant of the matrix of coefficients of a set of linear equations (see Cramer's rule).
That an associated locant number represents the location of a covalent bond in an organic compound, the position of which is variant between isomeric forms.
A simplex, simplicial complex, or convex hull.
In chemistry, the addition of heat in a reaction.
In legal shorthand, it represents a defendant.^[9]
In the financial markets, one of the Greeks, describes the rate of change of an option price for a given change in the underlying benchmark.
A major seventh chord in jazz music notation.
In genetics, it can stand for a gene deletion (e.g. the CCR5-Δ32, a 32 nucleotide/bp deletion within CCR5).
The American Dental Association cites it (together with omicron for "odont") as the symbol of dentistry.^[10]
The anonymous signature of James David Forbes.^[11]
Determinacy (having a definite truth-value) in philosophical logic.
In mathematics, the symbol ≜ (delta over equals) is occasionally used to define a new variable or function.^[12]

Lowercase

The lowercase letter δ (or 𝛿) can be used to denote:

A change in the value of a variable in calculus
A functional derivative in functional calculus
The (ε, δ)-definition of limits, in mathematics and more specifically in calculus
The Kronecker delta in mathematics
The degree of a vertex (graph theory)
The Dirac delta function in mathematics
The transition function in automata
Deflection in engineering mechanics
The force of interest in actuarial science
The chemical shift of nuclear magnetic resonance in chemistry
The relative electronegativity of different atoms in a molecule, δ⁻ being more electronegative than δ⁺
Text requiring deletion in proofreading; the usage is said to date back to classical times
In some of the manuscripts written by Dr. John Dee, the character of delta is used to represent Dee
A subunit of the F1 sector of the F-ATPase
The declination of an object in the equatorial coordinate system of astronomy
The dividend yield in the Black–Scholes option pricing formula
Ratios of environmental isotopes, such as ¹⁸O/¹⁶O and D/¹H from water are displayed using delta notation – δ¹⁸O and δD, respectively
The rate of depreciation of the aggregate capital stock of an economy in an exogenous growth model in macroeconomics^[13]
In a system that exhibits electrical reactance, the angle between voltage and current
Partial charge in chemistry
The maximum birefringence of a crystal in optical mineralogy.^[14]
An Old Irish voiced dental or alveolar fricative of uncertain articulation, the ancestor of the sound represented by Modern Irish dh

Unicode

U+018D ƍ LATIN SMALL LETTER TURNED DELTA
U+0394 Δ GREEK CAPITAL LETTER DELTA (Δ) (\Delta in TeX)
U+03B4 δ GREEK SMALL LETTER DELTA (δ) (\delta in TeX)
U+1D5F ᵟ MODIFIER LETTER SMALL DELTA
U+1E9F ẟ LATIN SMALL LETTER DELTA
U+2207 ∇ NABLA (&Del;, ∇)
U+225C ≜ DELTA EQUAL TO (&triangleq;, &trie;)
U+234B ⍋ APL FUNCTIONAL SYMBOL DELTA STILE
U+234D ⍍ APL FUNCTIONAL SYMBOL QUAD DELTA
U+2359 ⍙ APL FUNCTIONAL SYMBOL DELTA UNDERBAR
U+2C86 Ⲇ COPTIC CAPITAL LETTER DALDA
U+2C87 ⲇ COPTIC SMALL LETTER DALDA
U+1D6AB 𝚫 MATHEMATICAL BOLD CAPITAL DELTA^[a]
U+1D6C5 𝛅 MATHEMATICAL BOLD SMALL DELTA
U+1D6E5 𝛥 MATHEMATICAL ITALIC CAPITAL DELTA
U+1D6FF 𝛿 MATHEMATICAL ITALIC SMALL DELTA
U+1D71F 𝜟 MATHEMATICAL BOLD ITALIC CAPITAL DELTA
U+1D739 𝜹 MATHEMATICAL BOLD ITALIC SMALL DELTA
U+1D759 𝝙 MATHEMATICAL SANS-SERIF BOLD CAPITAL DELTA
U+1D773 𝝳 MATHEMATICAL SANS-SERIF BOLD SMALL DELTA
U+1D793 𝞓 MATHEMATICAL SANS-SERIF BOLD ITALIC CAPITAL DELTA
U+1D7AD 𝞭 MATHEMATICAL SANS-SERIF BOLD ITALIC SMALL DELTA

^ The MATHEMATICAL codes should only be used in math. Stylized Greek text should be encoded using the normal Greek letters, with markup and formatting to indicate text style.

References

^ "delta". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
^ "Dictionary of Standard Modern greek". Centre for the Greek Language.
^ "Definition of DELTA". www.merriam-webster.com. Retrieved 26 October 2017.
^ Celoria, Francis (1966). "Delta as a geographical concept in Greek literature". Isis. 57 (3): 385–388. doi:10.1086/350146. JSTOR 228368. S2CID 143811840.
^ Clarence H. Richardson (1954). An Introduction to the Calculus of Finite Differences. Van Nostrand. Chapter 1, pp. 1—3.online copy
^ Michael Comenetz (2002). Calculus: The Elements. World Scientific. pp. 73–74. ISBN 978-981-02-4904-5.
^ Dickenstein, Alicia; Emiris, Ioannis Z. (2005). Solving polynomial equations: foundations, algorithms, and applications. Springer. Example 2.5.6, p. 120. ISBN 978-3-540-24326-7.
^ Irving, Ronald S. (2004). Integers, polynomials, and rings. Springer-Verlag New York, Inc. Ch. 10.1, pp. 145. ISBN 978-0-387-40397-7.
^ Tepper, Pamela (2014). The Law of Contracts and the Uniform Commercial Code. Cengage Learning. p. 32. ISBN 978-1285448947. Retrieved 2018-04-30.
^ "Caduceus, the emblem of dentistry". American Dental Association. Archived from the original on 12 November 2012. Retrieved 26 October 2017.
^ Proceedings of the Royal Society, vol. XIX, p. ii.
^ "Who first defined the "equal-delta" or "delta over equal" symbol?". Archived from the original on 6 March 2022. Retrieved 2 October 2022.
^ "Faculty - Economics Department". econ.duke.edu. Retrieved 26 October 2017.
^ MACHADO, Fábio Braz, NARDY, Antônio José Ranalli (2018). Mineralogia Óptica. São Paulo: Oficina de Textos. p. 85. ISBN 9788579752452.{{cite book}}: CS1 maint: multiple names: authors list (link)

[15] The MATHEMATICAL codes should only be used in math. Stylized Greek text should be encoded using the normal Greek letters, with markup and formatting to indicate text style.

[1] "delta". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)

[2] "Dictionary of Standard Modern greek". Centre for the Greek Language.

[3] "Definition of DELTA". www.merriam-webster.com. Retrieved 26 October 2017.

[4] Celoria, Francis (1966). "Delta as a geographical concept in Greek literature". Isis. 57 (3): 385–388. doi:10.1086/350146. JSTOR 228368. S2CID 143811840.

[Richardson1954-5] Clarence H. Richardson (1954). An Introduction to the Calculus of Finite Differences. Van Nostrand. Chapter 1, pp. 1—3.online copy

[Comenetz2002-6] Michael Comenetz (2002). Calculus: The Elements. World Scientific. pp. 73–74. ISBN 978-981-02-4904-5.

[7] Dickenstein, Alicia; Emiris, Ioannis Z. (2005). Solving polynomial equations: foundations, algorithms, and applications. Springer. Example 2.5.6, p. 120. ISBN 978-3-540-24326-7.

[8] Irving, Ronald S. (2004). Integers, polynomials, and rings. Springer-Verlag New York, Inc. Ch. 10.1, pp. 145. ISBN 978-0-387-40397-7.

[9] Tepper, Pamela (2014). The Law of Contracts and the Uniform Commercial Code. Cengage Learning. p. 32. ISBN 978-1285448947. Retrieved 2018-04-30.

[10] "Caduceus, the emblem of dentistry". American Dental Association. Archived from the original on 12 November 2012. Retrieved 26 October 2017.

[11] Proceedings of the Royal Society, vol. XIX, p. ii.

[12] "Who first defined the "equal-delta" or "delta over equal" symbol?". Archived from the original on 6 March 2022. Retrieved 2 October 2022.

[13] "Faculty - Economics Department". econ.duke.edu. Retrieved 26 October 2017.

[14] MACHADO, Fábio Braz, NARDY, Antônio José Ranalli (2018). Mineralogia Óptica. São Paulo: Oficina de Textos. p. 85. ISBN 9788579752452.{{cite book}}: CS1 maint: multiple names: authors list (link)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[a]

Delta (letter)

Pronunciation

Uppercase

Lowercase

Unicode

See also

References