Identitat de Beltrami

La identitat de Beltrami, que porta el nom del matemàtic italià Eugenio Beltrami, és un cas especial de les equacions d'Euler-Lagrange en el càlcul de variacions.

Les equacions d'Euler-Lagrange serveixen per extremar l'acció de les funcions de la forma

${\displaystyle I[u]=\int _{a}^{b}L[x,u(x),u'(x)]\,dx\,,}$

on ${\displaystyle a}$ i ${\displaystyle b}$ són constants, i ${\displaystyle u'(x)={\frac {du}{dx}}}$.^[1]

Si ${\displaystyle {\frac {\partial L}{\partial x}}=0}$, llavors les equacions d'Euler-Lagrange es redueixen a la identitat de Beltrami,

${\displaystyle L-u'{\frac {\partial L}{\partial u'}}=C\,,}$

on C és una constant.^{[Nota 1][2]}

La següent derivació de la identitat de Beltrami comença amb l'equació d'Euler-Lagrange,

${\displaystyle {\frac {\partial L}{\partial u}}={\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.}$

Multiplicant els dos costats per u′,

${\displaystyle u'{\frac {\partial L}{\partial u}}=u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.}$

Segons la regla de la cadena,

${\displaystyle {dL \over dx}={\partial L \over \partial u}u'+{\partial L \over \partial u'}u''+{\partial L \over \partial x}\,,}$

on ${\displaystyle u''={\frac {du'}{dx}}={\frac {d^{2}u}{dx^{2}}}}$.

Reordenant això es produeixen

${\displaystyle u'{\partial L \over \partial u}={dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}\,.}$

Per tant, substituint aquesta expressió per ${\displaystyle u'{\frac {\partial L}{\partial u}}}$ en la segona equació d'aquesta derivació,

${\displaystyle {dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}-u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}=0\,.}$

Segons la regla del producte, l'últim terme es reexpressa com a

${\displaystyle u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}={\frac {d}{dx}}\left({\frac {\partial L}{\partial u'}}u'\right)-{\frac {\partial L}{\partial u'}}u''\,,}$

i reordenant,

${\displaystyle {d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)={\partial L \over \partial x}\,.}$

Per al cas de ${\displaystyle {\frac {\partial L}{\partial x}}=0}$, això es redueix a

${\displaystyle {d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)=0\,,}$

de manera prenen els resultats de l'antiderivada en la identitat de Beltrami,

${\displaystyle L-u'{\frac {\partial L}{\partial u'}}=C\,,}$

on C és una constant.^{[Nota 2]}

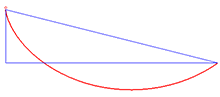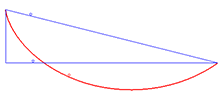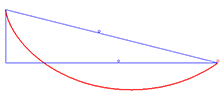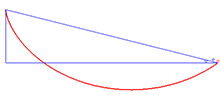
Un exemple d'aplicació de la identitat de Beltrami és el problema de la braquistòcrona, que consisteix a trobar la corba ${\displaystyle y=y(x)}$ que minimitza la integral

${\displaystyle I[y]=\int _{0}^{a}{\sqrt {{1+y'^{\,2}} \over y}}dx\,.}$

L'integrand

${\displaystyle L(y,y')={\sqrt {{1+y'^{\,2}} \over y}}}$

no depèn explícitament de la variable d'integració ${\displaystyle x}$, de manera que s’aplica la identitat de Beltrami,

${\displaystyle L-y'{\frac {\partial L}{\partial y'}}=C\,.}$

Substituint per ${\displaystyle L}$ i simplificant,

${\displaystyle y(1+y'^{\,2})=1/C^{2}~~{\text{(constant)}}\,,}$

que es pot resoldre amb el resultat posat en forma d'equacions paramètriques

${\displaystyle x=A(\phi -\sin \phi )}$

${\displaystyle y=A(1-\cos \phi )}$

amb ${\displaystyle A}$ sent la meitat de la constant anterior, ${\displaystyle {\frac {1}{2C^{2}}}}$, i ${\displaystyle \phi }$ essent una variable. Aquestes són les equacions paramètriques per a una cicloide.^{[Nota 3]}