|
EspectrogramaL'espectrograma o sonograma és una eina bàsica de representació que s’utilitza per a l’anàlisi dels senyals elèctrics, de comunicacions, i qualsevol senyal audiovisual en el seu contingut freqüencial. És una representació en tres dimensions, temps, freqüencial i amplitud de la distribució d’energia d’un senyal. La representació de l'espectre d'un senyal en el domini freqüencial, pot ajudar a entendre millor el seu contingut, que amb una representació en el domini temporal. L'espectrograma es pot interpretar com una projecció en dues dimensions d’una successió de Transformades de Fourier de trames consecutives, on l'energia i el contingut freqüencial del senyal va variant al llarg del temps. És una gràfica tridimensional que objectiva la variació de la freqüència d'un senyal en funció de la intensitat i del temps.[1] És una representació d'un senyal mostrat en una gràfica x-y. En el gràfic, l'eix vertical (y) representa la freqüència o to del soroll, expressat en kilohertz (kHz). Els sonogrames és representen en colors, l'arc de sant Martí dels colors mostra quan de fort està sent produïda una freqüència. Com més alt és el senyal, més proper a la zona vermella és. Els senyals molt baixos són propers a la zona blava. Els codis de colors per la intensitat dels senyals són molt útils per entendre com la intensitat varia dins d'un sonograma. Però tot i això, és necessari recordar que la intensitat disminueix quan ens allunyam de l'origen d'aquest. Com que els sonogrames es creen a partir de gravacions realitzades a distàncies variables des de la font, la intensitat representat en dos sonogrames diferents no pot comparar-se de manera directa.[2] Definició La construcció d'un espectrograma es basa en agafar un determinat nombre de mostres per mitjà d'una finestra temporal, amb una mida concreta. Segons el tipus d’anàlisi que es faci del senyal, harmònic o ressonant, la finestra haurà de tenir una mida determinada. A continuació es fa el càlcul del contingut freqüencial de les mostres enfinestrades, i es representen en una gràfica en tres dimensions. Seguidament es desplaça temporalment la finestra al llarg del senyal, per agafar un altre nombre de mostres diferents, es torna a calcular el contingut freqüencial i es torna a representar en la mateixa gràfica que l'anterior. Aquesta operació es va repetint successivament. La suma de la representació de les transformades de Fourier de les finestres consecutives, aporta informació de la variació de l'energia i la freqüència en funció del temps. La gràfica en tres dimensions pot ser representada de formes diferents, però la manera habitual de trobar-la és representant el temps en l'eix d'abscisses, representant les freqüències en l'eix d’ordenades i una representació de l'energia en dB en el pla tridimensional, aquesta acompanyada amb una gamma de colors que indiquen la variació en l'energia. CreacióL’anàlisi per trames és el primer pas a seguir en la creació d’un espectrograma, a causa de la naturalesa variant d’un senyal d’àudio, s’aplica una finestra per escollir un nombre limitat de mostres a processar. L'elecció de la finestra és un compromís entre la mida de la trama, el processat i l’anàlisi del senyal. Existeixen dos grans blocs de finestres anomenades de banda ampla Wideband i de banda estreta Narrowband. L’amplada de la finestra es considera en el domini freqüencial i fa referència a la resolució espectral del lòbul principal de la Transformada de Fourier de la finestra. És possible aplicar diferents tipus de finestra al senyal: Rectangular, Hanning, Bartlett, Blackman, Gaussiana, Kaiser, en són alguns exemples. Finestres amb amplada de banda grans en el domini temporal, suposen amplada de banda reduït en el domini freqüencial i finestres amb amplada de banda reduït en domini temporal, suposen amplada de banda gran en domini freqüencial. És per això que, segons el tipus de finestra escollida, serà possible aconseguir més o menys resolució en els lòbuls principals i secundaris de la Transformada de Fourier. STFT Un cop enfinestrat el senyal, es calcula de la Transformada de Fourier en Temps Discret (STFT) del conjunt de mostres enfinestrades. Sift és un mètode de processament de senyals no estacionàries en què les característiques estadístiques varien en funció del temps. Sift extreu diverses trames d'un senyal que són analitzades en cada un dels desplaçaments de la finestra al llarg del temps. El desplaçament de la finestra pot ser encavalcat per assegurar que les discontinuïtats que es produeixen entre trames no passin per alt i s’analitzin en el desplaçament de la trama següent, a aquest encavalcament de trames també se'l coneix com a overlap RepresentacióCada una de les trames que s’obtenen del càlcul del Sift s’indexen en una matriu.  Aquesta matriu representa la variació en l'espectre i l'energia del senyal per cada una de la successió de trames al llarg del temps. A mesura que es van obtenint noves trames, es van indexant de forma consecutiva en la primera posició de la matriu, empenyent la trama anterior a la segona posició, i la segona a la tercera, i així successivament. D’aquesta manera es pot representar la variació de l'espectre del senyal i l'energia en funció del temps. Una manera de representació de l'espectrograma és: el temps en l'eix abscisses, successions consecutives de transformades de Fourier, en l'eix d’ordenades la freqüència expressada en Hz i representada com la meitat de l'espectre, ja que la transformada de fourier és periòdica i el seu espectre es repeteix al llarg del temps. I per acabar, la representació de l'energia expressada en db com el mòdul de l'amplitud de la Transformada de Fourier [20*log10(abs(X(f))] i representada amb una paleta de colors, o amb nivells de gris, en el cas concret en l'escala de grisos, amb valors on l'energia és més gran representats amb uns nivells més foscos, i aquells valors on l'energia és més petita amb uns nivells més clars. CaracterístiquesL'elecció de la finestra dependrà del senyal a analitzar. A continuació es mostren les característiques de cadascuna. Narrow Band (Banda estreta)En fer l’anàlisi d'un senyal de música a través del seu espectre de la Transformada de Fourier s'observa que té un harmònic en la freqüència fonamental (fo), seguit d’uns quants harmònics secundaris que es troben distanciats a múltiples de la freqüència fonamental (2fo, 3fo…) l’amplada de banda que hi ha entre dos harmònics consecutius té, una mida a tenir en compte per calcular la mida de la finestra. En escala logarítmica els harmònics s’observen equidistants, i en escala lineal a la mateixa distància. En ser enfinestrat aquest senyal amb una longitud de trama petita, és a dir, agafant un nombre de mostres reduïdes per calcular la Sift, l’amplada de banda de la finestra serà prou reduïda, com perquè sigui més petit que l’amplada de banda que hi ha entre dos harmònics consecutius del senyal. D’aquesta manera, en fer la successió de transformades a cada desplaçament de la finestra, és possible visualitzar més detalladament l'estructura harmònica del senyal, quedant els harmònics més espaiats en la seva representació, i permetent així diferenciar millor entre cadascun d’ells. Per aquesta raó l'elecció d'una finestra de banda estreta serà més adequada per l’anàlisi de l'estructura harmònica d'un senyal.   Wideband (banda Ampla)Els espectrogrames de banda ampla són adequats per a una millor representació de l'estructura ressonant d'un senyal. Per exemple en un senyal de veu. L'elecció d'una finestra de banda ampla en l’anàlisi d'un senyal de veu en el seu contingut freqüencial, és pel fet que la seva estructura ressonant de la parla és més important que no pas el seu contingut harmònic, ja que la formació en les paraules per exemple una vocal, està relacionada amb la formació de les ones estacionàries que es provoquen en la cavitat ressonant d'una persona, que no pas en la informació de la seva estructura harmònica. El fet d'escollir una banda ampla comporta una representació més detallada en el contingut de l'estructura ressonant del senyal pel fet que el tracte vocal és més representatiu en la seva envolvent. Això té a veure amb què l’amplada de banda del lòbul principal de la finestra és prou gran per a encabir dos o més harmònics consecutius del senyal. D’aquesta manera la successió de Transformades de Fourier queda representada per l’amplitud de l'envolvent de la successió harmònica del senyal de veu. Per aquesta raó els espectrogrames calculats amb una banda ampla de finestra queden representats amb unes línies verticals corresponents a les ràpides variacions en l’amplitud del senyal  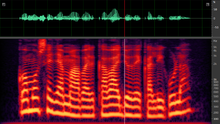 Aplicacions
Referències
Enllaços externs
|