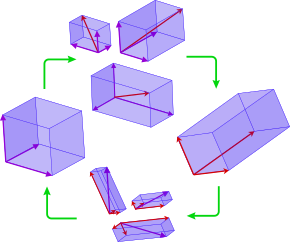
Canvi de base

Una combinació lineal d'una base de vectors (morat) resulta en un nou conjunt de vectors (vermell). Si aquests últims són linealment independents, llavors formen una nova base. Les combinacions lineals que relacionen el primer conjunt de vectors amb el segon s'estenen de forma natual a una transformació lineal, anomenada canvi de base.

Un vector es pot representar en dues bases diferents (fletxes morada i vermella).

En àlgebra lineal, una base d'un espai vectorial de dimensió n és un conjunt de n vectors α₁, ..., α_n amb la propietat que tot vector de l'espai es pot expressar de forma única com a combinació lineal dels vectors de la base. Les representacions matricials de les transformacions lineals també estan determinades per la base escollida. Com que sovint és convenient treballar amb més d'una base per un espai vectorial, té una importància fonamental disposar d'una eina per transformar de forma simple les representacions en coordenades de vectors i aplicacions respecte a una base a les seves representacions equivalents respecte a l'altra base. Una tal transformació d'una base a l'altra s'anomena canvi de base.

Tot i que emprarem la terminologia d'espais vectorials, i el símbol R pot representar el cos dels nombres reals, els resultats que veurem també són certs si R és un anell commutatiu i substituïm espai vectorial per R-mòdul lliure.

La base canònica per Rⁿ és {e₁, ..., e_n}, on e_j és l'element de Rⁿ que conté un 1 a la j-sima posició i 0 altrament.

Si T: Rⁿ → R^m és una transformació lineal, la matriu m × n de T és la matriu t que té T(e_j) per j-sima columna, on j = 1, ..., n. En aquest cas, tenim T(x) = tx per tot x en Rⁿ, on considerem x com a vector columna, i la multiplicació del segon membre de la igualtat és la multiplicació de matrius. És un resultat bàsic en àlgebra lineal que l'espai vectorial Hom(Rⁿ, R^m) de totes les transformacions lineals de Rⁿ a R^m és naturalment isomorf a l'espai R^{m × n} de matrius m × n sobre R; és a dir, una transformació lineal T: Rⁿ → R^m és, a tots els efectes, equivalent a la seva matriu t.

Ara utilitzarem la següent observació:

Aquesta T única es defineix per T(x₁α₁ + ... + x_nα_n) = x₁γ₁ + ... + x_nγ_n. Òbviament, si {γ₁, ..., γ_n} és una base de W, llavors T és bijectiva i lineal; en altres paraules, T és un isomorfisme. Si, en aquest cas, també tenim que W = V, llavors hom diu que T és un automorfisme.

Sigui ara V un espai vectorial sobre R, i suposem que {α₁, ..., α_n} és una base de V. Per definició, si ξ és un vector de V, llavors ξ = x₁α₁ + ... + x_nα_n on els escalars x₁, ..., x_n únics de R s'anomenen coordenades de ξ respecte a la base ordenada {α₁, ..., α_n}. El vector x = (x₁, ..., x_n) de Rⁿ s'anomena la tupla de coordenades de ξ (respecte a aquesta base). L'única aplicació lineal φ: Rⁿ → V amb φ(e_j) = α_j per j = 1, ..., n s'anomena isomorfisme coordenat per V i la base {α₁, ..., α_n}. Així, φ(x) = ξ si i només si ξ = x₁α₁ + ... + x_nα_n.

Un conjunt de vectors es pot representar per una matriu, les columnes de la qual són les components de cada vector del conjunt. Com que una base és un conjunt de vectors, una base es pot representar per una matriu formada d'aquesta manera. Després veurem que el canvi de base de qualsevol objecte de l'espai està relacionat amb aquesta matriu. Per exemple, els vectors canvien amb la seva inversa (i, per tant, s'anomenen objectes contravariants).

Primer examinarem la qüestió de com canvien les coordenades d'un vector ξ, de l'espai vectorial V, quan seleccionem una altra base.

Això significa que, donada una matriu M que té en columnes els vectors de la nova base de l'espai (nova matriu base), les noves coordenades per un vector columna v estan donades pel producte matricial M^-1·v. Per aquesta raó, hom diu que els vectors normals són objectes contravariants.

Qualsevol conjunt finit de vectors pot representar-se per una matriu que tingui per columnes les coordenades dels vectors donats. En dimensió 2, n'és un exemple un parell de vectors obtinguts mitjançant rotació de la base canònica 45 graus en sentit antihorari. La matriu que té en columnes les coordenades d'aquests vectors és

${\displaystyle M={\begin{pmatrix}1/{\sqrt {2}}&-1/{\sqrt {2}}\\1/{\sqrt {2}}&1/{\sqrt {2}}\end{pmatrix}}}$

Si volem canviar qualsevol vector de l'espai a aquesta nova base, només hem de multiplicar per l'esquerra les seves componentes per la inversa d'aquesta matriu.

Per exemple, considerem una nova base donada pels seus angles d'Euler. La matriu de la base té per columnes les components de cada vector. Per tant, aquesta matriu serà:

${\displaystyle [\mathbf {R} ]={\begin{bmatrix}\mathrm {c} _{\alpha }\,\mathrm {c} _{\gamma }-\mathrm {s} _{\alpha }\,\mathrm {c} _{\beta }\,\mathrm {s} _{\gamma }&-\mathrm {c} _{\alpha }\,\mathrm {s} _{\gamma }-\mathrm {s} _{\alpha }\,\mathrm {c} _{\beta }\,\mathrm {c} _{\gamma }&\mathrm {s} _{\beta }\,\mathrm {s} _{\alpha }\\\mathrm {s} _{\alpha }\,\mathrm {c} _{\gamma }+\mathrm {c} _{\alpha }\,\mathrm {c} _{\beta }\,\mathrm {s} _{\gamma }&-\mathrm {s} _{\alpha }\,\mathrm {s} _{\gamma }+\mathrm {c} _{\alpha }\,\mathrm {c} _{\beta }\,\mathrm {c} _{\gamma }&-\mathrm {s} _{\beta }\,\mathrm {c} _{\alpha }\\\mathrm {s} _{\beta }\,\mathrm {s} _{\gamma }&\mathrm {s} _{\beta }\,\mathrm {c} _{\gamma }&\mathrm {c} _{\beta }\end{bmatrix}}.}$

Novament, qualsevol vector de l'espai es pot canviar a aquesta nova base, tot multiplicant per l'esquerra les seves components per la inversa d'aquesta matriu.

Suposem que {α₁, ..., α_n} i {α'₁, ..., α'_n} són dues bases ordenades de V. Siguin φ₁ i φ₂ els corresponents isomorfismes coordenats (aplicacions lineals) de Rⁿ a V, és a dir, φ₁(e_j) = α_j i φ₂(e_j) = α'_j per j = 1, ..., n.

Si x = (x₁, ..., x_n) és la n-tupla de coordenades de ξ respecte a la primera base, de manera que ξ = φ₁(x), llavors la tupla de coordenades de ξ respecte a la segona base és φ₂^-1(ξ) = φ₂^-1(φ₁(x)). Ara bé, l'aplicació φ₂^-1 ∘ φ₁ és un automorfisme de Rⁿ i per tant té una matriu p. Addicionalment, la columna j-sima de p és φ₂^-1 ∘ φ₁(e_j) = φ₂^-1(α_j), és a dir, la n-tupla de coordenades de α_j respecte a la segona base {α'₁, ..., α'_n}. Per tant, y = φ₂^-1(φ₁(x)) = px és la n-tupla de coordenades de ξ respecte a la base {α'₁, ..., α'_n}.

Suposem que T: V → W és una transformació lineal, {α₁, ..., α_n} és una base de V i {β₁, ..., β_m} és una base de W. Siguin φ i ψ els isomorfismes coordenats de V i W, respectivament, en relació a les bases donades. Aleshores l'aplicació T₁ = ψ^-1 ∘ T ∘ φ és una transformació lineal de Rⁿ a R^m, i per tant té una matriu t; la seva columna j-sima és ψ^-1(T(α_j)) per j = 1, ..., n. Hom anomena aquesta matriu la matriu de T respecte a les bases ordenades {α₁, ..., α_n} i {β₁, ..., β_m}. Si η = T(ξ), i y i x són les tuples de coordenades de η i ξ, llavors y = ψ^-1(T(φ(x))) = tx. Recíprocament, si ξ pertany a V i x = φ^-1(ξ) és la tupla de coordenades de ξ respecte a {α₁, ..., α_n}, i igualem y = tx i η = ψ(y), llavors η = ψ(T₁(x)) = T(ξ). És a dir, si ξ pertany a V i η pertany a W, i x i y són les seves respectives tuples de coordenades, llavors y = tx si i només si η = T(ξ).

Ara ens plantegem què succeeix amb la matriu de T: V → W quan canviem les bases de V i W. Siguin {α₁, ..., α_n} i {β₁, ..., β_m} bases ordenades de V i W respectivament, i suposem que tenim un segon parell de bases {α'₁, ..., α'_n} i {β'₁, ..., β'_m}. Siguin φ₁ i φ₂ els isomorfismes coordenats, prenent la base habitual en Rⁿ, de la primera i la segona base de V, i siguin ψ₁ i ψ₂ els isomorfismes, prenent la base habitual en R^m, de la primera i segona base de W.

Siguin T₁ = ψ₁^-1 ∘ T ∘ φ₁, i T₂ = ψ₂^-1 ∘ T ∘ φ₂ (totes dues aplicacions porten Rⁿ a R^m), i siguin t₁ i t₂ les seves respectives matrius. Siguin p i q les matrius dels automorfismes de canvi de coordenades φ₂^-1 ∘ φ₁ de Rⁿ i ψ₂^-1 ∘ ψ₁ de R^m.

Les relacions de totes aquestes aplicacions s'il·lustren amb el següent diagrama commutatiu:

${\displaystyle {\begin{array}{rcl}\mathbb {R} ^{n}&{\stackrel {T_{1}}{\longrightarrow }}&\mathbb {R} ^{m}\\{\scriptstyle \varphi _{1}}\downarrow &&\downarrow {\scriptstyle \psi _{1}}\\V&{\stackrel {T}{\longrightarrow }}&W\\{\scriptstyle \varphi _{2}}\uparrow &&\uparrow {\scriptstyle \psi _{2}}\\\mathbb {R} ^{n}&{\stackrel {T_{2}}{\longrightarrow }}&\mathbb {R} ^{m}\\\end{array}}}$

Com que T₂ = ψ₂^-1 ∘ T ∘ φ₂ = (ψ₂^-1 ∘ ψ₁) ∘ T₁ ∘ (φ₁^-1 ∘ φ₂), i com que la composició d'aplicacions lineals correspon a la multiplicació de matrius, d'aquí se segueix que

t₂ = q t₁ p^-1.

Com que el canvi de base conté una vegada la matriu base i una vegada la seva inversa, hom diu que aquests objectes són 1-co, 1-contra-variants.

Un cas important de matriu d'una transformació lineal és el d'un endomorfisme, és a dir, una aplicació lineal d'un espai vectorial V a ell mateix; en altres paraules, el cas en què W = V. Podem prendre de manera natural {β₁, ..., β_n} = {α₁, ..., α_n} i {β'₁, ..., β'_m} = {α'₁, ..., α'_n}. La matriu de l'aplicació lineal T és necessàriament quadrada.

Apliquem el mateix canvi de base, de manera que q = p i la fórmula de canvi de base esdevé

t₂ = p t₁ p^-1.

En aquesta situació, la matriu invertible p s'anomena matriu de canvi de base per l'espai vectorial V, i l'equació anterior indica que les matrius t₁ i t₂ són semblants.

Una forma bilineal d'un espai vectorial V sobre un cos R és una aplicació V × V → R que és lineal en ambdós arguments, és a dir, B: V × V → R és bilineal si les aplicacions

${\displaystyle v\mapsto B(v,w)}$

${\displaystyle v\mapsto B(w,v)}$

són lineals per tot w de V. Aquesta definició és vàlida també per mòduls sobre un anell commutatiu, on les aplicacions lineals són homomorfismes de mòduls.

La matriu de Gram G associada a la base ${\displaystyle \alpha _{1},\dots ,\alpha _{n}}$ es defineix per

${\displaystyle G_{i,j}=B(\alpha _{i},\alpha _{j}).\,}$

Si ${\displaystyle v=\sum _{i}x_{i}\alpha _{i}}$ i ${\displaystyle w=\sum _{i}y_{i}\alpha _{i}}$ són les expressions dels vectors v, w respecte a aquesta base, llavors la forma bilineal ve donada per

${\displaystyle B(v,w)=v^{\mathsf {T}}Gw.\,}$

La matriu és simètrica si la forma bilineal B és una forma bilineal simètrica.

Si P és la matriu invertible que representa el canvi de base de ${\displaystyle \alpha _{1},\dots ,\alpha _{n}}$ a ${\displaystyle \alpha '_{1},\dots ,\alpha '_{n}}$ llavors la matriu de Gram transforma mitjançant la congruència de matrius

${\displaystyle G'=P^{\mathsf {T}}GP.\,}$

En teoria d'espais vectorials abstractes, el concepte de canvi de base és innocu; sembla que aporta poc valor a la ciència. Tot i això, hi ha casos en àlgebres associatives en què un canvi de base pot simplificar notablement un problema donat:

• En el pla dels nombres complexos hiperbòlics existeix una "base diagonal" alternativa. La hipèrbola estàndard xx − yy = 1 esdevé xy = 1 després del canvi de base. Les transformacions del pla que deixen invariants les hipèrboles es corresponen l'una amb l'altra, llevat d'un canvi de base.

• Per matrius reals 2 × 2, hom troba un catàleg d'àlgebres lineals creat per Arthur Cayley. El seu company James Cockle impulsà en 1849 la seva àlgebra de coquaternions, que és la mateixa àlgebra que la de matrius reals 2 × 2, només que expressada en una base diferent. Novament, el concepte de canvi de base relaciona l'àlgebra matricial de Cayley amb els coquaternions de Cockle.

• Un canvi de base transforma una matriu complexa 2 × 2 en un biquaternió.

• Transformada integral, l'anàleg continu del canvi de base.
• Transformació activa i passiva

• MIT Linear Algebra Lecture on Change of Bases, del MIT OpenCourseWare